Az alábbi írás egy módszertani szemlélet rekonstrukciós kísérlete. A Magyar Királyi Országos Mintarajztanodában és Rajztanárképezdében a XIX. század utolsó harmadában olyan rajztanítási gyakorlatot dolgoztak ki, amely - bár né mileg módosított formában - az I. világháborúig az oktatás törzsanyagát ké pezte. Az 1871 és 1914 között megrendezett nemzetközi rajzoktatási kiállítások fennmaradt dokumentációi tanúsága szerint az intézmény szellemi egyedülál lóságát nem a tananyag forradalmi jellege, hanem egy módszertani újítás, ne vezetesen a részegységek, a különálló tantárgyak összekapcsolásának módja je lentette. Az 1912-es drezdai IV. Nemzetközi Rajzoktatásügyi Kongresszuson és Kiállításon az akkor már Országos Magyar Királyi Képzőművészeti Főiskola cí met viselő tanintézet egyöntetű sikert ért el. A geometriai ismereteken alapu ló rajztanítás módszertanára vonatkozó rekonstrukciós kísérlet kulcselemei je lennek meg a kiállítási anyagot illető reflexiókban és az akkor ábrázoló geo- metriát, ékítményes rajzot, látszattant és szemléleti látszattant oktató Erdőssy Bélának a vallás és közoktatásügyi miniszterhez írott jelentésében. Ebben a kö vetkezőképpen vélekedik más nemzetek rajzoktatásáról:

"...mint logikusan feldolgozott rendszer többek közt teljesen hiányzik például a szabadkézi látszattan, szemléleti rajz, a térformák rajzolásának tanítása. Van ugyan itt-ott ennek is nyoma, de nem mint tervszerű anyagösszeállításnak, hanem úgyszólván mint keresgélése a tanítás menetének.

Ez a rendszer pedig fontos, mert alapját képezi nemcsak a szakoktatásnak, hanem a középfokú rajzoktatásnak is. Ennek a hiányát a külföldiek is nagyon érezhették, mert mindenféle nemzetbeli rajzoktató érdeklődött a nálunk már rég meglevő erre szolgáló modellek s azok beszerzési módja iránt."¹

A külföldi tanintézmények órarendjéből annyira hiányolt szemléleti látszattan önálló tantárgyként 1878-1879-ben került a tanítandó tárgyak körébe. A drezdai kiállítás külföldi elismeréseinek egyike szintén a - szakmában akkoriban példa nélkülinek tűnő - módszertani koncepcióra vonatkozik:

"SCHREINER A. stuttgarti tanárt, mint építészt főleg a magyar Rajztanárképző építészeti és geometriai tananyaga érdekelte s nagyon helyesnek tartja azt, hogy a szabadkézi rajz s a konstruktiv ábrázolás között szoros kapcsolat van s megjegyezte, hogy ezen elvet iskolájában is meghonosítja."²

A német építész-tanár a gyakorlati szemléleti látszattant (mint szabadkézi rajzot) az elméleti jellegű geometriával kapcsolatban említette, s kiemelte a magyar felsőfokú rajzoktatás fontos sajátosságát, a tantárgyak szoros kapcsolatát, s az egymásra épülő, egymást fedő tananyagok összefonódását.

Az alakrajzot, a művészeti bonctant és a mozdulati kompozíciót a Székelytanítvány Tardos-Krenner Viktor oktatta az 1910-es években. 1914-es, látásról írt - egyéb tekintetben kissé zavaros - fejtegetése egyben rajztanítási modellnek is tekinthető mind a részismereteket, mind a módszertant illetőleg. Az általa megfogalmazott látás(ok), tudásanyagok gyakorlatilag a főiskola akkor oktatott tantárgyainak feleltethetők meg.³

Tardos-Krenner szerint a rajzi látás egy olyan sokrétű, leíró jellegű, objektív látás, amely nélkülözhetetlen alapja a (szubjektív) művészi Zárásnak. A helyes rajzi látás számos, önálló egységként kezelt elemének összehangolt alkalmazásával sajátítható el. Ez a látás olyan "látásokból", illetve alkalmazásokból áll össze szerves egésszé, amelyek nagyrésze a térben megjelenő, ám két dimenzióban ábrázolandó tárgy(ak) egészére-felületére vonatkoznak. Ilyen a perspektivikus látás, amely "minden rajzi megbízhatóság" első feltétele. Az árnyékvetés ismerete és rajzi alkalmazása szintén fő szempontjainak egyike a "három-méretűség illúziójának felkeltéséhez". A tapintó látás, vagyis "a testek felületének, textúrájának helyes feltüntetése", valamint a korrekt színlátás is a tárgyegyüttesek egészére vonatkozó ismeretek. A részek, illetve a rész-egész kapcsolatait az élő testek anatómiáját és a tárgyak szerkezetét feltérképező anatomi-kus konstruktív látásban véli megnyilvánulni. Mindezekhez kapcsol még egy olyan "látást", amely érzelmi aspektusai révén már művészi természetű, de a látásnak még mindig objektív szeletében helyezkedik el. Ez "a mozdulat meglátása és annak rajzi ábrázolása".

A különálló elemek csak egymással teljes harmóniában alkothatják a helyes rajzi látást. Az imént felsorolt részismeretek a főiskolai tananyag egy-egy szaktárgyához köthetők. A részek egymástól és az egésztől való elválaszthatatlansá-ga az egyes tantárgyak közötti átjárhatóságban és a különböző órák bizonyos anyagrészeinek fedésében jutott kifejezésre. Kezdjük azokkal az ismeretekkel, amelyek a Képzőművészeti Főiskola egy-egy adott tantárgyának feleltek meg 1914-ben. "A mozdulat meglátását és annak rajzi ábrázolását" az alakrajzi mozdulat kompozíczió órán lehetett elsajátítani. Az anatomikus konstruktív látást a tanár- és tanítójelölteknek az állattanulmány és bonczalaktan, a művésznövendékeknek a művészeti boncztan elnevezésű órákon lehetett tanulni. A helyes színlátás a gyakorlati jellegű alakrajz és festés, a tapintó látás pedig a mintázás órák alapja volt.

A perspektivikus látás és az árnyékvetés ismerete, bár prioritásuk vitathatatlan, a sor végére került. A helyes rajzi látás ezen összetevői ugyanis - immár a fenti írástól elvonatkoztatva - több tantárgy anyagában is feltűntek egymással párhuzamosan az iskola fennállásának kezdeti éveitől fogva. Sőt, ha a geometriai tárgyak egymásra épülő anyagrészeit lineárisan tekintjük át, akkor a perspektíva elsajátítása, tudása, konstruktív (szerkesztő) és intuitív (szabadkézi) alkalmazása mint minden ismeretek koronája szerepelt. A Mintarajztanoda és Rajztanárképezdében a XIX. század utolsó harmadában az elemi és ábrázoló geometria, valamint a geometriai módszertan elnevezésű elméleti tárgyak sokkal több és szélesebb alapot fogtak át, mint az 1900-as, 1910-es években, amikor a mértani ismeretek egyre inkább a szemléletesség szolgálatába lettek állítva.⁴

Az imént említett, szűk értelemben vett geometriai tantárgyak pontos rekonstrukciója elegendő forrásanyag, óramenetek, óravázlatok, hallgatói rajzok híján nem kivitelezhető. Annál árnyaltabb összkép alkotható róluk, ha az iskola átfogó módszertani koncepciójának megfelelően más tárgyakkal együtt tekintjük át őket. Az alábbi táblázat a lineárisan (fentről lefelé tekintett) geometriai alaptárgyakat különböző anyagrészein át kapcsolja más és más gyakorlati órákhoz.

A tantárgykapcsolatok, egy átfogó rajzoktatási rendszer kialakítása már az iskola első tanéveiben megkezdődött. Erdőssy Béla 1912-es, fent említett kongresszusi jelentéséből az derült ki, hogy egy már rég meglevő rajztanítási szisztéma került bemutatásra a drezdai kiállításon. Az 1910-es években ábrázoló geometriát és látszattant oktató Kovách Géza 1928-ban megjelent, középfokú iskolák számára kidolgozott Illusztrált tanmenetének bevezetőjében szintén a XIX. század utolsó harmadára utalta a rendszeres rajztanítás születését, a koncepció körvonalazását pedig Székely Bertalan és Schulek Frigyes nevéhez kötötte.⁵ A tantárgykapcsolatok módszertani kidolgozása valóban csak olyan tanárok nevéhez fűződhetett, akik abban az időszakban több tantárgyat párhuzamosan adtak elő. E helyen természetesen csak a geometria és kapcsolódó tárgyainak tanításával foglalkozunk. Schulek Frigyes 1871-től 1902-ig egyszerre oktatta az építészeti rajzot, az építészeti stíl és alaktant, valamint a látszattant. Ékítmé-nyes rajzot valószínűleg 1871 és 1878 között taníthatott, valamint az iskola nyitó évében a látszattanon kívül az ábrázoló geometria is az ő hatáskörébe tartozott, hiszen a három geometriai alaptárgyat oktató Pórszász József csak 1872-től lépett be az intézmény tantestületébe. Schulekhez hasonló átfogó tanári tevékenységet az első három évtizedben még Várdai Szilárd végzett, igaz, eleinte csak segédtanári minőségben. Az 1878-1879-es tanévben ebben a pozícióban segédkezett Rauscher Lajosnak az ékítményes rajz és az iparművészeti rajz, valamint Schulek Frigyesnek a látszattan tanításában. Az 1885-1886-os tanévtől 1902-ig az ékítményes rajz tanára volt.⁶ A szemléleti látszattan mint önálló tárgy 1878-ban került az órarendbe, amelyet azelőtt sehol sem oktattak, "ma pedig a modern rajzoktatás egyik alapja" - írta Várdai 1908-ban, a főiskolai cím elnyerésének alkalmából megjelentetett iskolatörténeti összefoglalójában.⁷ Tanársegédként ő volt az, aki kidolgozhatta e gyakorlati tárgy menetét, s annak 1892-ig volt megbízott előadója, majd 1923-ig rendes tanára. 1888-1889-től mint az intézet metszet- és könyvtárának őre járult hozzá az átfogó tanterv kidolgozásához.⁸

A rekonstrukció forrásai az alábbi műcsoportok:

1. Fennmaradt hallgatói munkák 1871 és 1914 között.

2. Az iskola fennmaradt taneszközei.

3. Az intézmény szabályzati kivonatai, értesítői.⁹

4. Hazai és nemzetközi kiállítások fotódokumentációi 1871 és 1914 között.

5. Mintalapok a metszet- és könyvtárból.

6. A könyvtár vonatkozó szakkönyvei.

A diákok eredeti rajzait a mintalapokkal és a XIX. századi könyvritkaságok ábráival párhuzamba állítva mutatjuk be. A XIX. századból kevés iskolai rajzanyag maradt fenn, így az egyes tárgyak leírását esetenként korabeli, a könyvtár állományába 1900 előtt került azonos témájú szakkönyvek képanyagával illusztráljuk. Kifejezetten ábrázoló geometriai munkák csak az 1912-es drezdai tanügyi kiállítás mappáiban maradtak fenn, így a korábbi tanmenetek megfelelő fejezetei is csak ezekkel illusztrálhatok.

A továbbiakban a tantárgykapcsolatokat bemutató táblázat érintkezési pontjai mentén haladunk.

A geometriai tárgyak első részletes tanmenete az 1888-1889-es évkönyvben olvasható. Ennek teljes szövegét a jegyzetanyagban közöljük. A geometriai órák alapját az elemi geometria képezte, amely két nagy anyagrészt foglal magában, a planimetrial (síkgeometria) és a stereometriát (térgeometria). E két részt az első fennmaradt, 1878-1879-es évkönyv szerint akkor az előkészítő osztályban, 1888-ban pedig, a stereometriától elválasztva, az első osztályban tanították. A planimetria a síkbeli alapalakzatok tulajdonságainak leírásával és szerkesztéseivel foglalkozik.¹⁰ Gyakorlati alkalmazása két másik tárgyhoz, az ékítményes és az építészetirajz-órákhoz kötődik.

Az ékítményes rajz tantárgy két fő témája a síkékítmények és a domború dí-szítmények rajzoláson át történő megismerése volt.¹¹ Az utóbbi domború gipszöntvények mintáinak különféle technikákkal készült plasztikus ábrázolását, az előbbi a síkékítmények szerkesztését-rajzolását-festését jelentette. A tárgy ezen része a XIX. század utolsó harmadában szorosan kötődött a geometriai tárgyak alapját képező planimetriához. A síkékítmények szerkesztésénél a hallgatók kiválóan alkalmazhatták a planimetria-előadásokon elsajátított, síkmértani alapalakzatok szerkesztésére, illetve azok tulajdonságaira, belső törvényszerűségeire vonatkozó ismereteiket. A két tantárgy közötti kölcsönhatás eredménye látható a Magyar Királyi Iparművészeti Iskolának a mintarajziskola épületében 1894-ben megrendezett iskolai kiállításán. Az iparművészeti iskolában a mintaraj ztanodához hasonló szellemű képzés folyt, amint azt az 1900-as párizsi nemzetközi kiállítás fotódokumentációja is tanúsítja. Mivel a mintarajztanoda korai ékítményes rajzai nem maradtak fenn, ezért a tárgy oktatása egyrészt az iparművészeti iskola 1894-es kiállításának enteriőrfotói, másrészt külföldi mintarajzkönyvek képei segítségével rekonstruálható. A tízdarabos fotósorozat¹² egyikén Mértani síkékítmények felirattal egy álló paravánon végtelenített mintahálókat bemutató díszítményes mintalapok láthatók. A szerkesztett mezők feltételezhetően akvarell-technikával színezettek-festettek. A míves, dekoratív mintalapok alatt egy asztalon Szerkesztő planimetria megjelöléssel valószínűleg ezekkel kapcsolatos síkmértani szerkesztési gyakorlatok lehettek kiállítva. A mintarajztanodában oktatott planimetriai ismeretek később az ékítményes rajz közvetítésével voltak felhasználhatók az iparművészeti rajzórák önálló tervezési feladatainál.

Az ékítményes rajz tananyagának kidolgozása is külföldi - a könyvtár idevágó részét áttekintve főleg német - minták alapján történhetett. A XIX. század második felében a hagyományos díszítőmotívumok geometriai "felfejtésére" kétféle módszert dolgoztak ki. Az egyiknél a négyzethálót vagy annak egyszerűsített formáját, a ponthálót (csak a négyzetháló rácspontjait jelölve)¹³ alkalmazták. Ez a díszítmények mechanikus előállítását tette lehetővé, amelynek hátránya egyfelől az, hogy nem minden motívumra illeszthető egy ilyen rendszer, másfelől nem tárja fel a minták belső logikáját, előnye viszont egyszerűségében rejlik (122. kép). A másik eljárás a szerkesztés nehezebb, síkmértani tudást feltételező útja (124. kép). Az ornamensrajzolás alapjait tárgyaló könyvek javarésze természetesen mindkét módszert bemutatja.¹⁴ Közös vonásuk még a rajzoktatás alapjainak geometriai alapismeretekkel való kombinálása.¹⁵

Ez a szemlélet áthatotta a síkgeometriát felsőfokon taglaló összefoglaló műveket is. H. Becker 1905-ös Geometrisches Zeichen című műve például vegyesen mutat be könnyebb fajsúlyú módszerekkel megrajzolható díszítményeket, bonyolultabb szerkesztési lépésekkel előállítható, például egymást metsző görbékből álló ívekkel. Első fejezetében az eddigiekhez híven a négyzethálón alapuló elemeket mutatja be, majd a következőben már tisztán mértani alapokon a kúpszeletek, az ellipszis, a parabola, a hiperbola szerkesztését írja le, sőt tulajdonságaikra kitérve részletezi példaképpen a Pascal-Brianchon-tételt. Külön részben tárgyalja a különféle csúcsívek és egy másikban a gótikus mérművek szerkesztését. A görbéket, a spirálisokat, a csigavonalakat újfent a díszítmények-től elvonatkoztatva, szigorúan a síkgeometria határain belül tekinti át, majd beiktat egy szakaszt, amelyben a díszítőmotívumok stílustörténeti összegzését nyújtja (120., 121. kép). A főiskola könyvtára az általános rajzoktatáshoz kapcsolódva gazdag 1900 előtti díszítőművészeti anyaggal rendelkezik. Ezt a súlyozást valószínűleg nem a mértani síkékítményes rajzoknak az iparművészeti iskolában tapasztalt dominanciája, hanem a témának az 1870-es, 1880-as években történő általános virágzása indokolta.

Az építészeti stíl és alaktan-előadások gyakorlati párjaként szereplő építészetirajz-órák¹⁶ egyik típusfeladata volt építészeti részletek (oszlopfők, oszloprendek, építészeti tagozatok, kapuzatok, homlokzatok) kétnézetű rajzolása-szerkesztése. A különféle profilú párkányzatok metszetben való ábrázolását a síkgeometriai ismeretek alkalmazásával lehetett pontosan kivitelezni. Az épületdíszítő elemnek számító oszlopfők volutáinak megrajzolása is hasonlóan a vonatkozó planimetriai szerkesztésekkel történt. Becker fent idézett 1905-ös, síkgeometriai rajzokról írt művében nem kapcsolta össze módszertanilag a csigavonalak szerkesztését az építészeti elemek rajzolásával. Azonban a XIX. század második felében mégis születtek a rajztanítás módszertanát illetőleg olyan fantasztikus alapművek, amelyek az elemi és ábrázoló geometria minden, rajzi ábrázoláshoz köthető szeletét gyakorlati példákkal hozták összefüggésbe. Nicolaus Fialkowski több, a rajztanítást geometriai alapon tárgyaló összefoglaló művet írt mind a középfokú, mind a felsőfokú oktatás számára.¹⁷ Beckerrel szemben Fialkowski Die zeichnende Geometrie (Konstrukzions-Lehre) című ezerháromszáz ábrát tartalmazó tankönyve¹⁸ például a volutaszerkesztést az építészetre közvetlenül adaptálva ión és korinthoszi oszlopfők részletének szerkesztésével mutatta be (128. kép).

A stereometria a háromdimenziós térben lévő alakzatok tulajdonságait vizsgálja.¹⁹ 1878-1879-ben ezt az anyagrészt még a planimetriával együtt, az előkészítő osztályban tárgyalták, 1888-1889-ben pedig a mértani testek képzéséről és tulajdonságairól a merőleges vetületi ábrázolással összefüggésben az ábrázoló geometria keretén belül második évben tanulhattak a diákok.

Az ábrázoló geometriának alapítója, a francia matematikus, tengerészeti miniszter és haditengerészeti szakértő Gaspard Monge (1746-1818) megfogalmazásában a következő két feladatot kell szolgálnia:

"[Az ábrázoló geometria] művészetének két fő tárgya van: Az első a háromdimenziós testek szabatos ábrázolása a kétdimenziós rajzlapon úgy, hogy a rajz alapján a testek pontosan meghatározhatóak legyenek. Ebből a szempontból ez a nyelv a szellem emberének szükségeltetik, aki kigondol egy tervet azok számára, kiknek feladata a kivitelezés irányítása, és végül a mesterembereknek, akik munkája a különböző részek megvalósítása.

Az ábrázoló geometria második feladata mindannak kikövetkeztetése a testek pontos leírásából, ami szükségszerűen adódik formáikból és helyzetükből. Ebben az értelemben ez az igazság keresését jelenti; örökösen példákat nyújt az ismertből az ismeretlenbe történő átjárásra; és mivel ez mindig a legelemibb formájú tárgyakra alkalmazható, szükséges bevezetése a nemzeti tantervbe..."²⁰

Monge az Ecole Polytechnique, az európai oktatási rendszer számára példát képező híres műszaki felsőoktatási intézmény tanára és 1794-ben alapító tagjainak egyike volt. Mint a fenti idézetből is kiderül, a műszaki iskolák ábrázoló geometriai tananyaga némileg eltér egy a művészképzést és általános rajz-tanárképzést célul kitűző felsőoktatási iskoláétól. A mintarajztanoda rajztanárjelöltjeinek valóban szükséges volt a különféle ábrázolási elvek elsajátítása, azonban a művésznövendékeknek "csupán" annyira, amennyire a perspektíva és az árnyékábrázolás alapját képezte.

A geometriai ábrázolási rendszerek közül 1878-1879-ben az I. és II. évben az ábrázológeometria-órák keretén belül kettőt lehetett készségszinten elsajátítani: az orthogonális (merőleges) vetületi ábrázolást és az axonometriát.²¹ 1888-1889-ben ez már csak a II. évre szorítkozott és a perspektívaszerkesztés megalapozására jelöltetett.²²

Az ábrázoló geometria önálló tudományágként Monge tevékenysége óta létezik. Érdekes módon célkitűzései, alapelvei, módszerei a francia forradalom által megreformált iskolarendszerben egyre hangsúlyosabb szerepet kapó, merőben új szemléletű tantárgy előadásanyagából származnak. E tantárgyat még jóval a forradalom előtt Ábrázoló geometria néven Monge vezette be a mérnökképzés rendszerébe. Az 1748-ban alapított mézieres-i katonai akadémia tanársegédjeként 1768 és 1789 között erődítéstant oktatott. Előadásai keretében dolgozta ki önálló ábrázolási rendszerét, amelyet az általános geometriától való megkülönböztetés jeleként ábrázoló (vagy más szóval fordítva leíró) geometriának nevezett. A kőfaragók és ácsmesterek által alkalmazott rajzi módszerek vizsgálatával kezdte munkáját, és első ábrázoló geometriai elveit is e két területen próbálta ki. Az addigi bonyolultabb és hosszadalmas ábrázolási módszerek helyett az áttekinthetőbb és egyszerűbb, ma Monge-rendszerként ismert kétképsíkos ábrázolást ajánlotta. Előadásai már egy kiadható könyv terjedelmére rúgtak, ám annak publikálását a hatóságok, haditoknak nyilváníttatva, megtiltották. Előadásai először 1795-ben jelentek meg Géométrie Descriptive címmel. Az ábrázoló geometria önálló tudományággá szentelése Monge tanítványainak és közvetlen követőinek tevékenységén keresztül teljesedett be.²³ Monge ábrázoló geometriája erősen elméleti, tudományos alapokról építkező rendszer volt, amely a francia nemzeti műszaki rajzoktatás tantárgyaként számos követőre talált: ugyanabban az időben az esztétizáló, filozofikus jellegű német természettudományos kutatás is szívesen fogadta, sőt, a napóleoni időkben Egyiptomban is kiadták, Itáliában pedig már 1804-ben megjelent első fordítása. A brit rajzoktatásban azonban néhány elszigetelt kísérlet²⁴ után sem történt meg a Monge-rendszer teljes adaptálása. A francia kétképsíkos rendszer párjaként önállóan dolgozták ki az ortografikus - úgyszintén merőleges vetületekkel operáló - projekció (vetítés) elveit, amelynek első rendszeres leírását 1857-ben William Binns adta.²⁵ Újdonságértéke, miként Monge Ábrázoló geometriájáé is, abban rejlik, hogy az addig tapasztalati úton szerzett ismereteket rendszerezte és pontosította.

A XIX. századi kontinentális és brit geometriaoktatás közötti alapvető különbség a szemléletességben rejlik. Az azonos tárgyú angol könyvek előnyben részesítették a képies kifejezésmódokat, rajztankönyveikben is az egyszerűbb modellezési formákat választották.²⁶ A budapesti mintarajztanoda ábrázolási rendszereket felölelő tanmenete is valószínűleg sokban fordult ezen könyvek képiességre törekvő koncepciójához.²⁷ Az ortografikus (merőleges) projekciót (vetítés) tárgyaló brit művekben is következetesen megjelenik a szemléletesség elve. Binns az alapelemeket (pont-vonal-sík) és viszonyaikat tárgyakhoz kötötten magyarázza (126. kép). A geometriai elemek Monge rendszerében viszont absztrakt megfogalmazásban, képzelt síkok, egyenesek metszésvonalaiként, illetve metszőpontjaiként jelennek meg, nehezítve a rajz olvashatóságát (123. kép). Binns illusztrációiban valós tárgyak képzeletbeli helyzeteit rekonstruálja, mind a síklapú, mind a forgástestek esetében. Minden típusú térbeli alakzatot először speciális helyzetben tekint az ábrázolás tárgyának, úgy helyezi el azokat, hogy párhuzamosak legyenek a képsíkkal. A tárgyak általános, képsíkokhoz viszonyított ferde állása mindig a módszertani folyamat következő lépcsőfokán jelenik meg, nem úgy, mint Monge Ábrázoló geometriá]kban, ahol előadásai eleve egy általános, mindkét képsíkkal ferdeszöget bezáró egyenes projekciójával kezdődnek.

A képsíkra történő orthogonális (merőleges) és parallel vetítés, valamint a tárgyak ezúton nyert felül- és oldalnézetének egy rajzon, egymással összefüggésben való szerepeltetése az építészeti rajzok általánosan alkalmazott eszköze.(131. kép) A Monge-féle kétképsíkos rendszer a műszaki és az építészeti ábrázolás alapvető rendszere. Újdonságértéke nem az elv alkalmazásában rejlik, hanem az addig is ismert és a gyakorlatban elfogadott ábrázolás műszaki indítékú racionalizálásában és rendszerezésében. A monge-i geometria alaptétele -amely szerint a tér pontjai és vonalai (így az egyenes élekkel határolt testek is) meghatározhatók és leírhatók két, egymásra merőleges síkon feltüntetett vetületeik megadásával - valójában egy évszázadokkal azelőtt is alkalmazott rajzi eljárást ír le. Az elvet szisztematikusan felépített tananyagként vitte végig a pont-vonal-sík-test kapcsolataira és a geometriai testek különféle találkozásaira, illetve ábrázolásukra vonatkoztatva.

A merőleges vetületi ábrázolás egyrészt az épületek hossz- és keresztmetszeti rajzai, másrészt az épületdíszítő elemek két- vagy többnézetű megjelenítései kapcsán az építészeti rajzórák alapjává vált (63. kép). Az 1878-1879-es tanévben az "építészeti rajz- és styltanulmányok csak a 2-ik tanévben kezdődnek. Szükséges előzményei az 1-ső osztályban a mértani szakok és mértani rajz gya-korlása."²⁸ 1888-1889-ben, az eddig is megfigyelhető egyéves csúszásnak megfelelően, ez az anyagrész a II. évre, a kapcsolódó építészeti rajzi tanulmányok pedig a III. évre tolódtak.²⁹

A műszaki és az azzal összefüggésben álló építészeti rajzoknak kétféle kívánalomnak kell eleget tenniük. Képeiken az ábrázolandó tárgy rajza legyen szemléletes és olyan világos információkat nyújtson, amelyek lehetővé teszik az eredeti tárgy egyértelmű rekonstrukcióját. Az első látásra értelmezhető, egynézetű képek a szemléletességre (perspektíva, axonometria), a többnézetű, kétvagy többképsíkos rendszerek a rekonstrukció pontosságára törekednek (Monge-rendszer, ortografikus projekció).

A többnézetű rajzok, bármilyen logikusan és következetesen felépített ábrázolási rendszerben legyenek is előállítva, mindig nehezen értelmezhetők első látásra. Az imént körülírt rajzolvasási igény kettősségéből fakadóan a XIX. század első felében egy angol matematikus-tanár dolgozta ki az általa izometrikus-nak elnevezett perspektíva elveit, amely egyben az axonometria mint önálló ábrázolási rendszer történetének a kezdőpontját is jelenti. William Farish 1822-ben megjelent On Isometrical Perspective című művében a képiesség igényének eleget téve rendszerét egy szintén a képiesség követelményét maradéktalanul kielégítő hagyomány, a centrális perspektíva elméleti továbbgondolásával alakította ki.³⁰

Az axonometrikus kép szemléletesség szempontjából felveheti a versenyt a centrális vetítéssel szerkesztett képpel, sőt a műszaki rajzolás területén a re-konstruálhatóság követelményének megfelelve értékesebb leképezésnek minősül, mint az utóbbi. Ám a XIX. század erősen perspektíva alapú szemlélete miatt a század végéig nem válhatott sem az építészeti rajzok, sem a műalkotások alapvető képalkotási eszközévé. Ez a meggondolás tükröződik a tananyagban elfoglalt helyében és a tanítására fordított idő megállapításában. Az 1878-1879-es órarendben az orthogonális axonometria az orthogonális vetülettan részeként az I. év végén jelent meg a tananyagban, a II. évben pedig a klinogonális axonometria az árnyéktannal összefüggésben,³¹ 1888-1889-ben pedig már csak az orthogonális ábrázolás utolsó, összevont anyagrészeként a II. év végén.³² A XIX. század második felében számos olyan ábrázológeometriai-tankönyv jelent meg, amely az axonometriát önálló fejezetben tárgyalta és a főiskola állományába még 1900 előtt került.³³ A perspektíva prioritását szem előtt tartó, mindenre kiterjedő rajztanítási szemlélet azonban nem engedett elég teret ennek az ábrázolási módnak.

Az axonometria főiskolai oktatásban elfoglalt helyére jellemző még az 1912-es drezdai kiállításra összeállított anyag pár vonatkozó lapja. A hallgatói munkákat hét nagyméretű, lapozható mappába rendezték. Közülük a másodikban szerepel egy testcsoport axonometrikus képe annak merőleges vetületi ábrázolásaival összefüggésben (51. kép). A VI. kötetben Vegyes anyag összefoglaló cím alá kerültek axonometrikus rajzok (47. kép) intenzitási feladatokkal, torzfelületekkel, csavartestekkel és perspektívarekonstrukciókkal szomszédságban. A testek axonometrikus képe minden esetben orthogonális vetületeikkel összefüggésben szerepel.³⁴

A XIX. századi műszaki rajzolásban előszeretettel alkalmazták az axonometriát gépek, szerkezetek bemutatására, és az építészeti rajz sem haladt túl a szerkezeti elemek ilyenfajta megjelenítésén, az ábrázolást nem terjesztette ki az épületek látképeinek előállítására.³⁵ Az axonometria az építészeti rajzok egységes ábrázolási eszközeként elsőként August Choisy 1870-es, 1880-as években kiadott építészettörténeti összefoglalóiban jelent meg jellegzetes szerkezeti elemek, csomópontok illusztrálására (125. kép).³⁶ Azt, hogy a részletek, az illeszkedések axo-nometrikus ábrázolása ismert volt a főiskola építészeti rajzgyakorlati feladataiban, egy 1876-ból származó hallgatói munka bizonyítja. A Schulek-tanítvány Niklay János Sajt-tartó Boenigenben című rajzán a faház három vetülete (homlok-, oldalnézet és alaprajz) mellett a részletábrát axonometriában jelenítette meg (62. kép). Ez a fajta ábrázolási mód azonban az építészeti rajzórák anyagában nem nyerhetett nagyobb teret a perspektivikus és az orthogonális vetületi képek mellett. Az iskola könyvtárában az eddig áttekintett ábrázoló geometriai tárgyú mintalapok közül 1902-ből Josef Wildttől származik az axonometriát épületszerkezetek bemutatására alkalmazó összefoglaló mű.³⁷

A perspektívaszerkesztés hagyományosan az ábrázoló-geometria órák tananyagának része (129. kép). A főiskolán azonban ettől elválasztva külön tárgyként oktatták a látszattanórákon, amelyet 1871-től 1902-ig egységesen minden hallgatónak Schulek Frigyes tanított, 1878-1879-ben még távlat- és árnytanként a III. szakosztály számára, "Különösen az építészet köréből vett gyakorlati példák kíséretében"³⁸ Egy, a főiskola levéltárából előkerült 1882-1883-as kézzel írott órarend szerint akkor már látszattan volt az óra elnevezése.³⁹

Az 1888-1889-es értesítő tartalmazza a látszattam órák törzsanyagát. A harmad- és negyedévesek számára kötelezően előírt előadásokon a diákok a perspektívaszerkesztés elméleti részét sajátíthatták el, amely tulajdonképpen megfelel az ábrázológeometria-tankönyvek vonatkozó fejezeteinek.⁴⁰ A rajzórákon pedig vegyes, főként építészettel kapcsolatos szerkesztő rajzfeladatokat kellett kivitelezniük.⁴¹ A szerkesztő látszattan oktatása egységesen folyt egészen az 1897-1898-as tanévig, amikor megszületett a külön órarendekkel ellátott három szaktanfolyam: (1) a rajztanár- és rajztanítójelölteké, (2) a rajztanítónőjelölteké és a (3) művésznövendékeké ("leendő festészek és szobrászok"). A rajztanár- és rajztanítójelöltek az addigi rendszerben tanulták a geometriai és kapcsolódó tárgyakat, a rajztanítónők csökkentett óraszámban szűkített tananyagot sajátíthattak el, és a látszattani szerkesztéseket egyrészt az ábrázoló geometriai órákon harmadévben, másrészt a látszattani órákon negyedévben tanulták. A művésznövendékek hasonlóan csökkentett óraszámban és erősen szelektált tananyagot tanultak, ráadásul csak első- és másodévben.

A Schulek-tanítványok fennmaradt rajzai közül Zvér Ferenc faházat ábrázoló látképe készülhetett a látszattanórán (61. kép). Az órák anyagát az 1896-os ezredéves kiállításon építészeti és szabadkézi látszattani rajzokkal összefüggésben mutatták be (59. kép). A III-IV. évesek rajzfeladatait Schulek dolgozta ki, amelyek közül a fotórészleten az alsó sorban a következők ismerhetők fel: "ékített síkok centrális ábrázolása"; "síkok által határolt testek, forgási testek, testcsoportok ábrázolása" és "az építészet köréből vett tárgyak".⁴²

Az órák első típusfeladata az "ékített síkok centrális ábrázolása" volt. A hasonló szellemű iparművészeti iskola a mintarajztanoda épületében rendezett 1894-es kiállításának már idézett enteriőrfotóján ezek a rövidülésben megszerkesztett ékítményes felületek az ábrázoló geometria tárgyához tartoztak és a szerkesztő planimetria-mértani síkékítmények műcsoportokkal összefüggésben lettek kiállítva. A végtelenített mintahálókat síkban bemutató ékítményes tablók orna-mensrendszerei jelennek meg a látszattani rajzokon is. A geometrikus elemekből álló összefüggő padlózat rövidülésben történő ábrázolása egyben síkmértani alakzatok, négyszögek, sokszögek, körök torzulásának, illetőleg a torzulás mértékének matematikai vizsgálatát jelentették. Az iskola témába vágó könyvei között eddig nem került elő olyan mű vagy mintalapsorozat, amely a síkékítmények síkban és centrális perspektívában történő ábrázolását ilyen következetesen kapcsolta volna össze, mint ahogy azt az iparművészeti iskola és minden bizonnyal - bár az eltérő képzési profilból fakadóan nem annyira hangsúlyosan - a mintarajztanoda tanítási rendszerében tették. A rajztankönyvek azonos típusfeladatai általában megállnak a mértani alapalakzatok rövidülésben való szerkesztésénél és nem terjednek ki mintarendszerek centrális ábrázolására (127. kép).

Az árnyékvetés ismeretének tanítása több tárgyat átfogó feladat volt. Elméleti alapja megjelent az ábrázológeometria-órák anyagában a merőleges vetületi ábrázolás és az axonometria témaköröknél. Gyakorlati feladatként szerepelt egyrészt az ékítményesrajz-órák domború díszítményeinek plasztikus ábrázolásánál és ehhez kapcsolódóan az iparművészetirajz-órákon, másrészt a szemléletilátszattan-órákon. Ez utóbbiak elméleti alapját, nevezetesen az árnyékszerkesztés alapjait a látszattanórák nyújtották. Az erre vonatkozó típusfeladatot az "Árnyékszerkesztés természetes és mesterséges világítás feltétele mellett" fogalmazták meg a tanmenetben.⁴³ Eredeti rajzok híján itt ismét egy kiállításfotó-. ra támaszkodunk az 1900-as párizsi nemzetközi kiállítás dokumentációjából.⁴⁴ A kiállítóegység közepén a rendezők lapozható tárlókat helyeztek el, amelyek a Schulek-tanítványok képeinél voltak kinyitva perspektívaszerkesztés ("constructions de perspective") feliratozással. A mesterségesen megvilágított belső tereket ábrázoló és a természetes megvilágítás mellett született - modellek utáni - rajzok azt mutatják, hogy Schulek a perspektívaszerkesztés és az árnyékvetés elméleti ismereteit rögtön szemléletes gyakorlati példákon gyakoroltatta.

A szemléletilátszattan-órák egyértelműen a szabadkézi rajzolás fejlesztésére szolgáltak. Mégis ennél a tantárgynál kell részleteznünk az 1912-es drezdai kiállítás fennmaradt ábrázoló geometriai anyagának javarészét, hiszen az akkori kiállítás pozitív kritikai észrevételeinek egyike éppen a geometriai szerkesztések és a szabadkézi rajz összekapcsolásának módszerére vonatkozott.

A személeti látszattan (szabadkézi rajz) önálló tárgyként való bevezetése az 1878-1879-es tanévben történt meg, tanára (akkor még segédtanári minőségben) ifj. Várdai Szilárd volt. Várdai 1907-ig oktatta ezt a tárgyat az I. és II. osztályosok számára, 1894 és 1897 között pedig az a Kovách Géza segédkezett kisegítő tanárként a tanításban, aki az 1903-1904-es tanévtől kezdve a látszattannal összefüggésben tanított ábrázoló geometriát Pórszász József helyett a rajztanár- és rajztanítójelöltek számára.

A tisztánlátás végett álljon itt az 1897-1898-as iskolai tanév értesítőjének e tárgyra vonatkozó része:

"Szemléleti látszattan" és II. osztály. Heti 2-2 óra

Geometriai testek és ezekből összeállított csoportozatoknak, valamint építészeti alkatrészek és csendéletszerű motívumoknak pusztán szemlélet alapján való szabadkézzel való ábrázolása; gyakorlatok szén, kréta, ecset és ceruzával, gyors- és könnyed-kezelésben; fősúlyt fektetve a helyes látás érzékének fejlesztésére.

A rajzgyakorlatok kapcsán megismerése a legelemibb látszattani törvényeknek és azoknak gyakorlati alkalmazása. A vetett árnyékoknak részben közvetlen megfigyelés alapján való feltüntetése, részben szabad kézzel való megszerkesztése; az intenzitás fokozatainak hű ábrázolása, - természetes és mesterséges világítás mellett. Végül gyors vázolási gyakorlatok.

A kezdők tömegesen nagyméretű geometriai testek és testcsoportokról lehetőleg nagy arányokban rajzolnak, a haladók kisebb domború minták után különböző nagyságú rajzgyakorlatokat végeznek."⁴⁵

Az órarend szerint mind a három szaktanfolyam növendékei egységesen az I. és a II. évben tanulták a szabadkézi helyes látszati rajzolást. Azonban a rajztanár- és rajztanító jelöltek, valamint a rajztanítónő-jelöltek ennek elméleti megfelelőjét, az ábrázoló geometria vetületi ábrázolást és árnyékvetést bemutató egységét a II. évben, a szerkesztő látszattant pedig a III--IV. évben tanulták. A művésznövendékek a szemléleti látszattant, az ábrázoló geometriát és a látszattant párhuzamosan tanulhatták I-II. évben.⁴⁶

A szemléleti látszattan modelljei részben azonosak voltak a geometriai rajzórák modelljeivel. A tantárgy az 1902-1903-as tanév átfogó módosításaival megszűnt önálló tanegységként létezni. Helyét a csendélet-rajz és -festés elnevezésű óra vette át, amelynek I-II. osztályaiban a tananyagot alapfokon továbbra is a régi szemléleti látszattan képezte.

"Csendélet-rajz és festés. (Szemléleti látszattan)

Ezen tárgy főként a perspektivai látérzéket, a perspektivai elváltozások helyes megfigyelését s a természetből közvetlenül vett impressiók grafikus, helyes és gyors visszaadását fejleszti.

Az oktatás anyagát kezdőfokon - mely "Szemléleti látszattan" elnevezés alatt szerepelt eddig tantervünkben - a geometriai tárgyakból meríti. Mindazonáltal ezen tárgy tisztán szabadkézi rajz és festés-tanulmány, sok tekintetben a szerkesztő látszattant pótolja; de azért utóbbival össze nem téveszthető, mert ezen tárgy tulajdonképpen a helyes látást instruktiv módon a leghivatottabban fejleszti, miért is a művészi rajztanításban nélkülözhetetlen.

... ezen tárgy nem geometriai rajz jellegével bir ...

Indokolja ezen tantárgynak szélesebb alapon való gyakorlását azon körülmény is, hogy a modern rajzoktatás, és közelebbről a közép- és egyéb iskoláink újabb tanterve is a művészeti rajzoktatás főanyagául tűzi ki ezt.⁴⁷ [...]"

A térbeliség kétféleképpen érzékeltethető két dimenzióban: konstruktívan és intuitíve. Az előbbin mértani szerkesztést (1), az utóbbin szabadkézi rajzot (2) értünk. Ez utóbbi a szemléletilátszattan-órák sajátja volt, az előző a látszattan -és ábrázológeometria-óráké, azonban mindkettő egymással összekapcsolva jelent meg a szerkesztő jellegű gyakorlati órák anyagában.

Az 1890-es és 1900-as években a szemléletilátszattan-órákon tapasztalati úton szerzett perspektívaismeretek mintegy megelőlegezték a mértani szerkesztéseket:

"...A constructiv perspectivának a szemléleti látszattanban kitűnő előiskoláját bírjuk. Ezen két tantárgy intézetünkben állandó kölcsönhatásban tartatik; feladataink a haladottabb fokon is gyakran a szemléleti képből indulnak ki."⁴⁸

A kölcsönhatás mértékét igen jól jellemzi a harmadéves szerkesztő jellegű látszattanórák háromféle típusfeladata. Ezek közül csak az első tisztán geometriai szerkesztő gyakorlat, a másik kettő elegyíti a konstrukciót és a szabadkézi rajzot:

"1. Centralis ábrázolás a látszati képsíkon közvetlenül, modellek, stereometriai vagy grafikus adatok alapján.

2. Természet után vagy szabadon készült rajznak constructiv helyesbítése, bizonyos részletek helyességének föltételezése mellett.

3. Összetettebb objectumok stereometriai tömegeinek perspectivicus ábrázolása, az alárendelt részleteknek érzés útján való berajzolása, azaz a perspectivicus képnek szabad befejezése."⁴⁹

A geometriai és szabadkézi rajz módszertani összekapcsolására már a XIX. század második felében is történtek kísérletek.⁵⁰ A kétféle, egymással kombinált mód gyakorlati alkalmazásának rendszeres kidolgozása egyértelműen az intézet vezető tanárainak tevékenységéhez köthető. Az 1912-es drezdai kiállítás ábrázológeometriai-anyagából is az derült ki, hogy a hallgatók a kétfajta ismeretet kevert formában, egymást erősítve, párhuzamosan sajátították el. E módszertani koncepció következetes végigvitelének illusztrálására álljon itt a drezdai kiállítás teljes ábrázológeometriai-anyagának részletes leírása.

Egyedülálló rajzi anyag maradt fenn az ábrázoló geometria tanítására és a hallgatói munkákra vonatkozólag az 1912-es évből összesen hét kötetben az első-, másod- és harmadéves rajztanár- és rajztanítónő-jelöltek órai, otthoni és zárthelyi feladataiból. A kötetek technikailag egységes képet mutatnak. Az egyes gyakorlatok megoldásait sok esetben a szaktanár vagy segédje által megfogalmazott és megrajzolt litografált feladatlapok előzik meg. Ezt követik a tanár által meghatározott technikával kivitelezett kidolgozott lapok, amelyek általában háromféle eljárással, esetleg azok kombinálásával születtek meg: ceruzarajz, tus és (minden esetben egységesen kék színű) aquarell.

Az I. kötet (Az elméleti előadást kísérő parallel feladatok) egyrészt az orthogonális (merőleges) vetületi rajz (I. éves tananyag), másrészt a centrális vetítés (III. év) alapjait mutatja be.⁵²

A II. kötet (Síklapú testek árnyékszerkesztési és áthatási feladatokkal) síklapú geometriai modellek orthogonális (merőleges) ábrázolásait prezentálja két és három képsíkon az első év feladatai közül (48., 52. kép). A párhuzamos vetítés (parellel projekció) tárgykörébe tartozóan a feladatok közül az utolsók között szerepel egy geometriai testcsoport merőleges vetületeinek és axonometrikus képének egy rajzon való szerepeltetése(51. kép) , valamint egy stereometriai feladat.⁵³ A III. kötet (Forgásfelületek árnyékszerkesztési és áthatási feladatai) a II. éves tananyag hangsúlyos részét képező forgástestek merőleges vetületi ábrázolásait és árnyékszerkesztéseit foglalja össze (50. kép).⁵⁴

A IV. kötet (Az orthogonális és centrális vetületi szerkesztések kapcsolatban szabad látszati képek rajzolásával) önálló részt igényel. Ez a kötet közöl elsőként teljes terjedelmében olyan feladatokat, amelyek a geometriai és a szabadkézi rajz között teremtenek kapcsolatot. A szaktanár négyféle feladatot jelölt ki előre nyomott litográfiákban a hallgatók számára. Ezek közül az első három kivitelezése két, a negyediké négy különálló lapon történt. Mindegyik gyakorlat ugyanazt az elvet követte, csak egyre nehezebb, bővített formában (két képsík helyett három fölvétele stb.); nevezetesen mindegyik egy orthogonális (merőleges) vetületeiben megadott tárgy látszati képének szabadkézi előállítását célozta. Érdemes a 4. feladat tanári instrukcióinak pontos idézése: "1. Orthogonális projectiokban megadott összeállítás.

2. Ugyanennek szabad, látszati megrajzolása a horizont megadásával és a vilá- gitás szögének megadásával.

3. A látszati rendszer konstruktív megállapítása ugyanezen adatok alapján.

4. A szerkesztésileg megállapított kép artisztikus befejezése.

5. A szituáció föltüntetése az I. sz. orthogonális vetületi rajzon a 3. sz. alatt jel zett föltételek alapján."⁵⁵

Modellként építészeti alkatrészeket használtak, amelyeket a fentiek megoldásaként a következőképpen ábrázoltak: az 1. képen a tárgy három merőleges vetülete látható tussal és aquarell-technikával kivitelezve. A 2. képen ugyanannak a tárgynak szabad kézzel előállított ceruzarajza, a harmadikon a szerkesztett látszati kép (tussal és akvarellel kidolgozva), a negyediken pedig szintén szabadkézi látszati rajza szerepel (ceruza, fedőfehér). Ezt a kötetet az elv további, a szemléleti látszattanra történő közvetlen adaptációjaként táji környezetben megjelenített épületrészek vízfestményeivel zárták. Ezek egyikén egy templomtorony festői ábrázolása mellett annak tussal kihúzott, orthogonális vetületi szerkesztése látható a bal felső sarokban külön papíron előállítva, az eredeti festménybe utólag belevágva.

Az V. kötet (Testcsoportok orthogonális és centrális projectiokban) másod-éves diákok munkáinak olyan válogatása, ahol ugyanazon tárgyegyüttesek merőleges vetületi nézeteit és perspektív képét külön lapokon jelenítették meg (53 kép). A VI. kötetben Vegyes anyag: axonometrikus képek (47. kép), intenzitási feladatok (49. kép), torzfelületek, csavartestek, perspektívarekonstrukciók láthatók. A VII. kötetben (Vetületek alapján szabadlátszati-rajz készítés, továbbá perspektivikus kép megszerkesztése [az utóbbi mint zárthelyi dolgozat, a perspecti-vai tanulmányi idő felének elteltével]) a IV. kötet már részletezett, a geometriai szerkesztés és szabadkézi rajz kapcsolatát hangsúlyozó feladatsor ismétlése az elv fontosságát és tanításban elfoglalt hangsúlyos helyét illusztrálja (54. kép).

Mind ez idáig egy, a rajztanítás módszertanára vonatkozó rekonstrukciót kíséreltünk meg. Paradox módon a geometriatanítás módszertanára vonatkozó órákat az 1902-1903-as tanévben teljesen törölték a tanrendből. A tárgyat egyébként 1872-től 1902-ig Pórszász József oktatta a IV. osztály számára heti két órában, tanítási gyakorlatokkal egybekötve. A középiskolai tanítás módszertana mellett az ábrázoló geometriának egyéb tudományágakkal határos területeit, így a geográfiához és a geodéziához kapcsolódó térképészet és tereprajzolás ismereteit is áttekintették. Az 1897-1898-as tanévtől kezdve a három szaktanfolyam hallgatói közül csak a rajztanár- és rajztanítójelöltek számára volt kötelező ez az elméleti tárgy.

<< Vissza     Tovább >>

120. Geometrikus hálóminták. In Becker, H.-Vonder- linn J.: Geometrisches Zeichnen. Leipzig, 1905. Taf. 6.

121. Geometrikus hálóminták. Uo., Taf. 7.

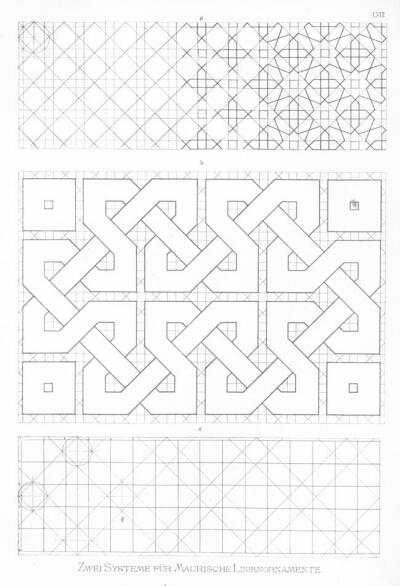
122. Mór vonaldíszrendszerek. In Andel, A.: Das Geometrische Ornament Wien, 1877. LVIII.

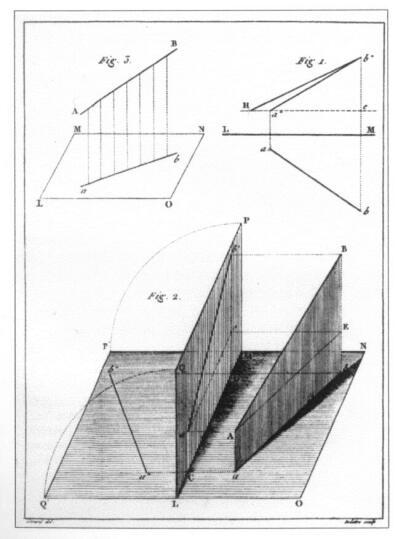
123. Egyenes merőleges vetületi ábrázolása két képsíkon. In Monge, G.: Geometrie Descriptive. Paris, 1798. Fig. 2.

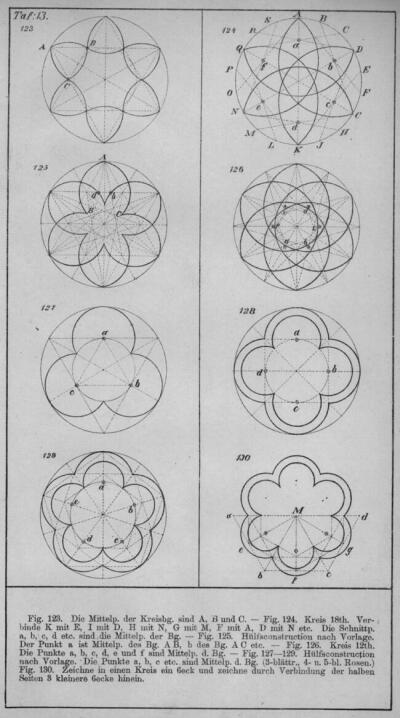
124. Síkmértani szerkesztések. In Baer, J.-Dreesen, G.: Das Geometrische Zeichnen.... Flensburg, 1882. Taf. 15.

125. Építészeti részlet axonometrikus képe. Illusztráció A. Choisy L'art de bâtir chez les Romains című művéhez, 1873.

126. Ház ortografikus projekciója. In Binns, W.: An Elementary Treatise on Ortographic Projection... London, 1857. Fig.la.

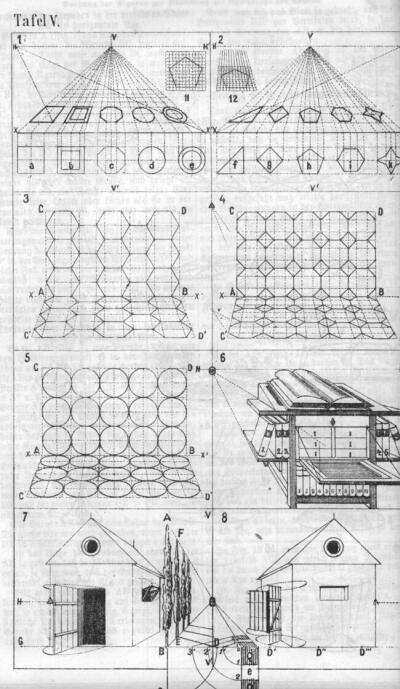
127. Síkmértani alapelemek szerkesztése centrális perspektívában (fent). In Fialkowski, N.: Freies Auffassen und Zeichnen Wien, 1873. Tafel V.

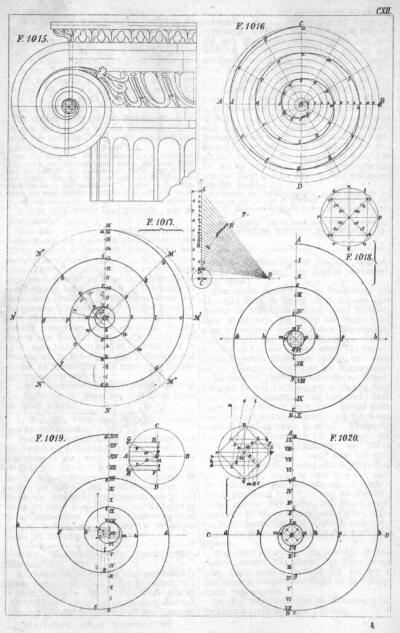
128. Ión voluta szerkesztése. In Fialkowski, N.: Die zeichnende Geometrie (Konstrukzions-Lehre). Wien, 1860. CXII.

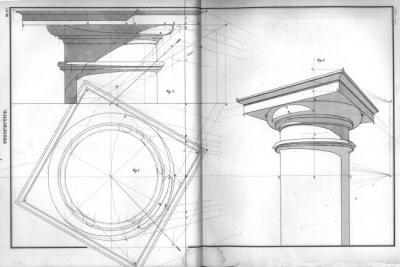
129. Oszlopfőmerőleges vetületei és perspektivikus képe árnyékszerkesztéssel. In Leroy, G: Atlas zu C. F. A. Leroy's Stéréotomie. Stuttgart, 1861. Bl. 27.

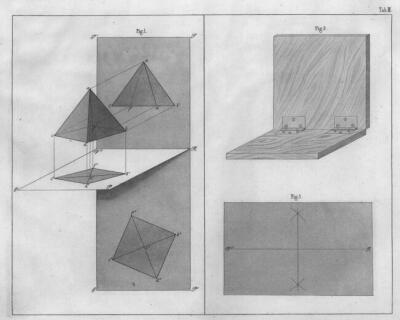
130. Gúla merőleges vetületi ábrázolása (Fig.l.) és a két képsík szemléltetése (Fig.2.). In Müller, J.: Die Constructive Zeichnungs-Lehre... Braunschweig, 1865. Tab. II.

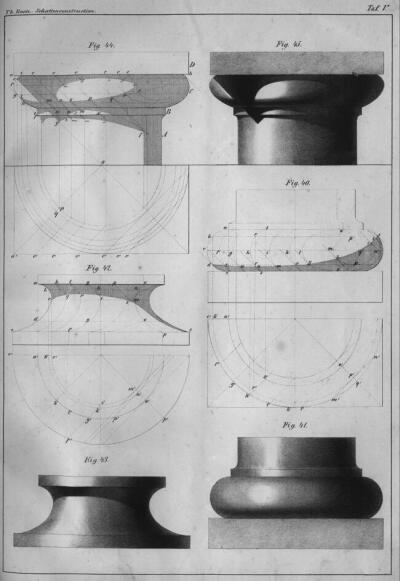
131. Oszlopfő és lábazat (mint forgástestek) merőleges vetületi ábrázolása az önárnyék jelölésével. In Raetz, Th.: Praktische Anleitung zur Schatten-Construction... Berlin, 1864. Taf. V.

1 Az Orsz. M. Kir. Képzőművészeti Főiskola Évkönyve az 1912-1913 tanévről, szerkesztette Várdai Szilárd igazgató-tanár, ifj. Kellner Ernő könyvnyomdája, Bp., 1915, 6.

2 Uo, 8.

3 Tardos Krenner Viktor, A látás, kézirat, 1914, Magyar Kézpőművészeti Egyetem Levéltára, Iktatott iratok 1907-1915, 1/b.

4 A geometriai tágyakkal kapcsolatban mindig problémák merültek fel. Az elemi és ábrázoló geomet riát, valamint a geometriai módszertant 1872-től 1902-ig Pórszász József tanította. A diákok egyenlőtlen felzárkózása miatt számos alkalommal volt szükség tanrenden kívüli tanfolyamok beiktatására, amelye ket Kovách Géza tartott 1890-től 1897-ig egységesen, szaktól függetlenül minden diáknak, majd 1897-1898-ban csak a nőhallgatóknak, 1898-tól 1902-ig pedig a művésznövendékek számára. Az 1902-1903-as tanév radikális változásokat hozott a geometriaoktatásban, eltörölték a geometriai módszer tant, és az elemi geometriát is fakultatív tárggyá minősítették, amelynek előadásával Pórszász Józsefet bízták meg. Az "...ábrázoló geometriát összefüggőleg a látszattannal Kovách Géza tanár adja elő, a val lás- és közoktatási miniszter úr f. évi 37,318. számú rendeletével PÖRSZASZ JÓZSEF tanárt segédtaná ri működése alól felmentette..." Az Országos M. Kir. Mintarajziskola és Rajztanárképző Értesítője az 1902- 1903. tanévről, közli Várdai Szilárd h. igazgató, Franklin-társulat nyomdája, Bp., 1903, 57-58.

5 "Rajzoktatásunk rendszeres fejlődése az 1871-i évvel, az Orsz. m. kir. Mintarajziskola és Rajztanárkép ző megnyitásával vette kezdetét. Ezen időtől fogva lassanként képzett szakemberek foglalták el iskoláink rajzi tanszékeit, melyeket addig avatatlan, vagy hiányos felkészültségű egyénekkel töltöttek be, ha ugyan a rajztanításról egyáltalában történt gondoskodás. A Rajztanárképző nagy mestereinek, Székely Bertalan nak és Schulek Frigyesnek irányítása jelölte meg rajzoktatásunk számára a haladás útját." Illusztrált tan menet a középfokú iskolák rajztanítása számára, készítette Kovách Géza az Orsz. Képzőművészeti Főisko la nyug. tanára, Kir. Magy. Egyetemi nyomda, Bp., 1928, 7.

6 A főiskola 1939-1941-es évkönyvében az 1871 és 1941 közötti időszakra összesített tanári névsor sze rint Várdai 1878 és 1892 között az ékítményes rajz megbízott előadója, 1892 és 1923 között pedig a tárgy rendes tanára volt. Az Orsz. M. Kir. Képzőművészeti Főiskola Értesítője, 1939/40, 1940/41, Attila nyom da, Bp., 1941, 11, 14.

7 Várdai Szilárd, Az Orsz. M. Kir. Mintarajziskola és Rajztanárképző története 1871-1908, in Az Orszá gos M. Kir. Képzőművészeti Főiskola Értesítője az 1907-1908. tanévről, közli az igazgatóság nevében Vár dai Szilárd igazgató-tanár., Ifj. Kellner Ernő könyvnyomdája, Bp., 1908, 3-42.

8 A tanárokra vonatkozó adminisztratív adatok forrásai A Magyar Királyi Országos Mintarajziskolának és Rajztanárképzőnek évente kiadott Értesítői/Évkönyvei (a továbbiakban Értesítő), amelyek az 1870-es évekből nem maradtak fenn minden tanévre vonatkozóan.

9 Lásd 8. jegyzet: az Értesítők/Évkönyvek állandó alcíme: "Az intézet czélja, szervezete és tantervének, valamint a rajztanárvizsgálati szabályzat kivonatával közli..."

10 "PLANIMETRIA / Heti 4 óra ea. és 2 óra rajzolás az I. oszt. számára. / 1. A térelemek (pont, egye nes) relatív vonatkozásai és az idomok képzése általában. / 2. Az alapidomok (véges egyenes, kör, szög, öv) helyzeti és metrikus tulajdonságai. / 5. A főidomok, és pedig: / A) az egyenes vonaluak (pont- és su gársor, tört egyenes, 3-, 4- és sokszög) alkotó részei, projectivitása (congruens és axialis symmetria, ha sonlóság és centrikus symmetria, collineatio és involutió), transversálisai és területe. / B) a görbe és ve gyes vonaluak, és pedig: / a) A kör, vonatkozások a térelemek és az előbb tárgyalt idomokhoz (projecti- vikus, potentialis, polárikus és harmonikus tulajdonságok), kerület és terület. / b) A kúpszeletek elemei. / c) A cycloisok, evolvensek és az alkalmazott csigavonalak leírása. / Constructiv föladatok az egész tárgy körből." Értesítő, 1888-1889, 9-10.

11 "ÉKÍTMÉNYES RAJZ / I. osztály. Heti 8 óra. / Síkékítmények rajzolása tömeges tanítás mellett, kü lönös tekintettel a jellegzetes összefoglalható formák gyors felvázolására. Domború ékítmények rajzolása, a különböző rajzszerek és anyagok kezelésében, valamint a különböző előadási módokban való gyakorla tok. / Geometriai síkékítmények, harmonikus szin összeállítási gyakorlatok. / II. osztály, heti 8 óra. / Folytatása a domború mintákról való rajzolásnak, továbbá síkdíszítményi tanulmányok főleg a görög és re-naissance stílben. Tervezési gyakorlatok." Értesítő, 1897-1898, 9.

12 Felvételek a m. kir. iparművészeti iskola 1894. évi kiállításáról., tíz darab, Magyar Képzőművészeti Egyetem Könyvtára, ltsz. 5072.

13 Schopp's Zeichenschule, Frankfurt, 1871. A mű tárgyszavai a könyvtár 1900-ban megjelent címjegyzé kében: "Pontjelzett rajzminták."

14 Andel, A., Das Geometrische Ornament, Verlag von R. v. Waldheim, Wien, 1877; Baer, J.-Dreesen, G., Das Geometrische Zeichnen mit besonderer Berücksichtigung des geometrischen Omaments für den Unterricht, Aug. Westphalen, Flensburg, 1882; Becker, H.-Vonderlinn J., Geometrisches Zeichnen, G. J. Göschen'sche Verlagshandlung, Leipzig, 1905; Sauer, W., Raumlehre und Zeichnen in Verbindung, Július Imme's Verlag, Berlin, 1874; Schreiber, G., Zum Ersten Unterricht im Zeichnen, Verlag von J. Veith, Carlsruhe, 1864.

15 Lásd 14. jegyzet, Andel és Sauer művei.

16 "II. ÉPÍTÉSZETI STÍL ÉS ALAKTAN. / III. osztály. Heti 8 óra. / I. Elmélet. / ... / II. Gyakorlat. / a) Építészeti részletek rajzolása az előadás után készített vázlatok és mintalapok alapján árnyékszerkesz tésekkel, egyszerűbb feladatok önálló kidolgozása. / b) Részletes tanulmányok rajzolása az ó-kori classicus- és a renaissance építészet köréből válogatott minták nyomán. / c) (Műhelyi rajz). Építőipari tárgyak kivitelének alapjául szolgáló rajzok készítése megfelelő méretekben, a különböző szerkezetek feltüntetésével." Értesítő, 1897-1898, 8-9.

17 Fialkowski, N., Freies Auffassen und Zeichnen der Gegenstande nach der Natúr oder nach der Anschauung, Selbstverlag des Verfasser, Wien, 1873.

18 Fialkowski, N., Die zeichnende Geometrie (Konstrukzions-Lehre), Verlag der Wallishauffer'schen Buchhandlung, Wien, 1860.

19 "2. ÁBRÁZOLÓ GEOMETRIA / A) STEREOMETRIA és ORTHOGONÁLIS ÁBRÁZOLÁS / Heti 6 óra ea. és 2 óra rajzolás a II. osztály számára / 1) STEREOMETRIA / 1. A térelemek (pont, egyenes és sík) relatív vonatkozásai és az idomok képzése általában. / 2. Az alapidomok (kitérő (torz) egyenespár, pont és sík, egyenes és sík, lapszög, réteg és testszög) helyzeti és metrikus tulajdonságai. / 3. A főidomok, és pedig / A) a síklapúak (szögletes testek) (hasáb, gúla és polyeder) alkotó részei, transversális síkjai, congruentiája és axiális symmetriája, hasonlósága és centrikus symmetriája, felülete és köbtartalma. / B) a görbe és vegyeslapúak (gömbölyű testek) (henger, kúp és gömb) alkotórészei, transversális síkjai, congruentiája és axiális symmetriája, hasonlósága és centrikus symmetriája, felülete és köbtartalma. / Constractiv feladatok az egész tárgykörből." Értesítő, 1888-1889, 10.

20 Monge, G., Géométrie Descriptive, Lecons données aux Écoles Normales, Baudoin, Paris, 1798, 5. Az idézet a szerző fordítása.

21 "ÁBRÁZOLÓ MÉRTAN (I-ső szakosztály.) / I. Orthogonális vetülettan. (Hetenkint 3 óra előadás és 4 óra rajzolás.) Az elemi téralakok ábrázolása. Az elemi téralakok relativ fekvésére vonatkozó feladatok. La pos idomok, szögletes testek, görbe vonalak és görbe lapok ábrázolása; metszések és érintések. Az axono metria. / II. Klinogonális vetülettan. (II. szakosztály.) Axonometria és árnyéktan. (Hetenkint 2 óra előadás és 4 óra rajzolás.)" Értesítő, 1878-1879, 5.

22 "ÁBRÁZOLÓ GEOMETRIA / A) STEREOMETRIA és ORTHOGONÁLIS ÁBRÁZOLÁS / Heti 6 óra ea. és 2 óra rajzolás a II. osztály számára / 2. ORTHOGONÁLIS ÁBRÁZOLÁS / 1. Bevezetés és alapfo galmak. Ábrázolás egy és több képsíkon; a felező síkok. / 2. A térelemek ábrázolása. / 3. A térelemek re lativ vonatkozásai, különösen metszések, távolságok és szögek. / 4. A sík idomok ábrázolása. / 5. A testek (hasáb, gúla, henger, kúp és forgási testek) ábrázolása; relativ vonatkozások a térelemekkel és egymással. / 6. Megvilágítási szerkesztések, u.m. vetett és saját árnyék, a megvilágítás intensitása. / 7. Idomok hely- zettransformátiói; képsíktransformátiók. / 8. Az orthogonális és klinogonális axonometria elemei. / Const- ructiv feladatok az egész tárgykörből. / Jegyzet A 6. és 7. pontban foglaltak alkalmilag tárgyaltatnak." Értesítő, 1888-1889, 11. Az orthogonális vetületi ábrázolás tanítása a perspektíva merőleges vetületek se gítségével történő szerkesztését alapozta meg, amelyre a látszattani órák keretén belül került sor a III. osztályban.

23 Monge közvetlen követői: Lacroix, S. F., Essai de géométrei sur les plans et les surfaces courbes, 1795; Hachette, J. N. P., Applications de géométrie descriptive, Paris, 1817; Dupin, Ch., Applications de géométrie et de méchanique a la marine, aux ponts et chaussées, etc, Paris, 1822; Olivier, Th., Cours de géomét rie descriptive, Paris, 1843.

24 A főiskola ábrázoló geometriai témájú könyvei közül eddig nem került elő eredeti, XVIII-XIX. századi Monge-mű, annál több a rendszer későbbi, főleg német adaptációi közül. Thomas Bradley 1840-ben tartott előadássorozatot Monge ábrázoló geometriájáról a londoni King's College-ban. A kiadott előadás anyag nagyméretű, szemléletes mintalapokkal még 1900 előtt került a könyvtár állományába, Binns alap- művéhez hasonlóan: Bradley, Th.-Hall, T. G., The Elements of Descriptive Geometry, London, 1840; Binns, W., An Elementary Treatise on Ortographic Projection, being a new method of teaching the Science of Mechanikai Engineering Drawing, London, 1857.

25 Uo.

26 Lásd Vere Foster's drawing copy-books, Simpkin, Marshall, London, [1900 előtt]. A mű tárgyszavai a könyvtár 1900-ban megjelent címjegyzékében: "Rajzoktatási tanmenetek. Az elemi oktatástól kezdve az emberi alak rajzolásáig. Angol rajzfüzetek: növény, táj, állati és emberi alakok rajzmintái; mértani szer kesztések és géprészletek." 32 füzet közös tokban.

27 Néhány, a könyvtárban található jelentős, angol középfokú rajz- és geometriaoktatási tankönyvek, módszertani útmutatók közül: Carroll, J., Practkal Geometry for Science and Art Students, London, 1888; Barfield, T. C, Model Drawing and Shading from Casts, Chapman & Hall, London, 1896; Davidson, Ellis A., Ortographic and isometrical projection- development of surfaces and penetration of solids, Cassell Petter & Galpin, London, ca. 1910.

28 Értesítő, 1878-1879, 4.

29 "Építészeti rajz- és stiltanulmányok heti 8 órában csak a III. osztályban kezdődnek. / Szükséges előzményöket képezi a megelőző két osztályban szerzendő geometriai ismeret és rajzbeli gyakorlottság. / Mű szaki rajzgyakorlatok, előkészítésül a műépítészeti alaktanra. Árnyékszerkesztés, intenzitási gyakorlatok...." Értesítő, 1888-1889, 7-8.

30 Farish, W., On Isometrical Perspective, Cambridge Philosophical Society Transactions, Vol. I, 1-20, 1822.

31 Lásd 21. jegyzet.

32 Lásd 22. jegyzet.

33 Güntner, K., Lehrbuch der darstellenden Geometrie mit eingehender Anleitung zur Schattenkonstruk- tion, Linear-Perspective und axonometrischen Darstellung für Realschulen und zum Selbstunterricht, Sallmaner und Comp., Wien, 1862; Delabar, G., Anleitung zum Linearzeichnen j 2. Theil, 3. Abtheil: Die Polar- und Parallel-Perspective, Freiburg, 1870; Staudigl, R., Die Axonometrische und Schiefe Projection (Parallal-perspective) / Ein Lehrbuch für technische Schulen und zum Selbst-Studium, Verlag von L. W. Seidel und Sohn, Wien, 1875.

34 A tanintézet egyre erősödő perspektíva alapú szemléletére jellemző volt, hogy 1897-től, a három szaktanfolyam bevezetésének évétől kezdve az addigi teljes tananyagot csak a rajztanár- és rajztanító-jelöltek nek kellett tanulniuk. A rajztanítónő-jelöltek és művésznövendékek csökkentett óraszámban szűkített geo metriai ismereteket sajátíthattak el. Ráadásul a mindkét szaktanfolyam számára előírt ábrázoló geomet riai órák anyagából hiányzott az axonometria tanítása. Csak a perspektívaszerkesztéshez szükséges, az orthogonális vetületi ábrázolásra és az árnyékszerkesztésre szorítkozó törzsanyagnak jutott hely (lásd Ér tesítő, 1897-1898, 19-20, 24). Sőt, az 1902-1903-as tantervi módosítások következtében a geometriaórák számának általános redukálása azt eredményezte, hogy attól a tanévtől kezdve a művésznövendékek szá mára nem tartottak külön ábrázoló geometriaiórákat, hanem a szükséges alapismereteket a szemléleti lát szattan és a látszattaniszerkesztés-órák vonatkozó anyagrészeinél tárgyalták {Értesítő, 1902-1903, 49).

35 Ez az ábrázolási mód csak a XX. században terjedt ki az építészeti látképekre is. Az axonometria az 1920- as években Théo van Doesburg tevékenysége nyomán vált az építészeti rajz általános formájává. Lásd Moravánszky, A., Az axonometria mint szimbolikus forma, in Perspektíva, Műcsarnok, Bp., 2000, 193-203.

36 Choisy, A., L'art de batir chez les Romains, Ducher, Paris, 1873; Uő, L'art de batir chez les Byzantine, Société Anonyme, Paris, 1883; Uő, Histoire de l'architecture, Gautier-Villars, Paris, 1898-1899.

37 Wildt, L, Praktische Beispiele aus der darstellenden Geometrie für Lehranstalten mit bau- oder kunst-gewerblicher Richtung, Verlag von A. Pichler's Witwe & Sohn, Wien, 1902.

38 Értesítő, 1878-1879, 4.

39 Az orsz. m. kir. mintarajztanoda és rajztanárképezdének az 1882j3iki Ilik tanfélévre tanártestületileg megállapított Tanóra-rendje, MKF Levéltár, Iktatott iratok 1871-1906 1/b.

40 "B. CENTRÁLIS ÁBRÁZOLÁS (perspectiva, látszattan) / Heti 2 óra előadás és 2-8 óra rajzolás, a III. és IV. osztály számára. / Bevezetésül: látszati képek szerkesztése az orthogonális ábrázolási mód alapján. / I. Elméleti rész / 1. A térelemek (pont, egyenes és sík) centrális ábrázolása és helyzeti megállapítása egy síkon. / 2. A térelemek helyzeti vonatkozásai: metsző egyenesek, két sík metszése. / 3. A térelemek méretes vonatkozásai: [...] / 4. Segédmíveletek korlátolt képsíkon, összevonási középpont alkalmazása, összevont segédkép, egyenlőközű egyenesek képének szerkesztése enyészőpont nélkül. / 5. Különféle mértékegységek és lépték rendszeres alkalmazása, hálók. / 6. Az elnyulások és visszás helyzetek határai. / 7. A kör és más sík görbék centrális ábrázolása." Értesítő, 1888-1889, 11-12.

41 "II. Gyakorlati rész / Heti 2-8 óra rajzolás leginkább a IV. osztály számára / 1. Ékített síkok centrá lis ábrázolása. / 2. Síkok által határolt testek, forgási testek, testcsoportok ábrázolása. / 3. Az építészet kö réből vett tárgyak. / 4. Árnyékszerkesztés természetes és mesterséges világítás feltétele mellett. / 5. Tü körképek a tükör síkjának különböző állásai mellett. / 6. Adott látszati képek kifejtése (visszafejtése) és hibáinak javítása. / 7. Látszati képek tervezete." Értesítő, 1888-1889, 12.

42 Lásd 41. jegyzet.

43 Uo.

44 Erdélyi Mór, Az 1900. párisi nemzetközi kiálítás magyar osztályából, 1900 k., két darab, Magyar Kép zőművészeti Egyetem Könyvtára, ltsz. 3783.

45 Értesítő, 1897/98, 10-11.

46 Értesítő, 1897/98, 92-94.

47 Értesítő, 1902/03, 32-33.

48 Értesítő, 1902/03, 42.

49 Értesítő, 1902/03, 42-43.

50 Bölter, J. W., Das Freihandzeichnen nach geometrischen Körpern und Gypsmodellen, Verlag von Huber u. Comp., St. Gallen, 1865; Vogeler, S. H., Anleitung zum Zeichnen der einfachen Kó'rperformen, H. Meyer, Halberstadt, 1871; Calame, A., Lecons de Paysage, Francois Delarue, Paris.

51 Königliche ungarische Hochschule für Zeichenlehrerbildung in Budapest, I-VIL, IV. Nemzetközi Rajz oktatásügyi Kiállítás, Drezda, 1912. A mappák belső borítóján kézírással a címben szereplő magyar nyel vű mondat áll.

52 "I. kötet: Az elméleti előadást kísérő parallel feladatok / 1. Orthogonális ábrázolás egy képsíkon / 2. Orthogonális ábrázolás két és több képsíkon / 3. Síkidomok árnyéka (orthogonális vetületben) / 4. A kör és a kerülék árnyéka / 5. Szabályos egyenes gúlák projectioinak megszerkesztése / 6. A henger mint mértani hely / 7. Feladatok a gömbhöz / 8. Feladatok a pont centrális ábrázolásához / 9. Feladatok a sík nyom- és irányélének megkereséséhez / 10. Egyenesvonalú síkidomok, hálók látszati képei / 11. Az egye nes áthatása síkon."

53 "II. kötet: Síklapú testek árnyékszerkesztési és áthatási feladatokkal / 1. A képsíkkal szöget bezáró sík- lapú test orthogonális (merőleges) vetületi ábrázolása két képsíkon / 2. Hasábok és gúlák orthogonális (merőleges) vetületei két képsíkon árnyékszerkesztéssel kombinálva / 3. Tárgyegyüttesek orthogonális (merőleges) vetületei két képsíkon árnyékszerkesztéssel kombinálva / 4. Árnyékszerkesztési gyakorlatok / 5. Képsíkkal szöget bezáró test orthogonális (merőleges) vetületi ábrázolása két képsíkon árnyékszerkesz téssel / 6. Képsíkkal szöget bezáró testcsoport orthogonális (merőleges) vetületi ábrázolása két képsíkon árnyékszerkesztéssel / 7. Testcsoport orthogonális (merőleges) vetületi ábrázolása árnyékszerkesztéssel há rom képsíkon / 8. Testcsoport orthogonális (merőleges) vetületi ábrázolása két képsíkon és axonometri- kus képe / 9. Stereometriai gyakorlat."

54 "III. kötet: Forgásfelületek árnyékszerkesztési és áthatási feladatai / 1. Forgásfelületek árnyékszerkesz tési feladatai / 2. Forgástestek áthatása."

55 Lásd IV. kötet.